What's behind Automerge? (Part I)
Runtime
Operation Set
Operation Set (OpSet), as the name suggested, is a set of operations. It is the runtime data structure of Automerge, that enables the creation, retrieval, updating, and deletion of objects. The merging of two documents is conceptually the union of two operation sets.
Everytime we update, delete or create an object, we insert an operation into the OpSet. And the retrieval of an object is actually the retrieval of an operation of the OpSet.
Every operation in the operation set is associated with a timestamp which indicates the causal order of the operation. We use <couter, actorID> as the timestamp, which is a Lamport clock. In Automerge, the term “actor” is used instead of “replica”, but the two are essentially interchangeable. For the remainder of the document, we will refer to the timestamp of an operation as OpId (Operation ID).
Every Map or List object has an object ID, which is the OpId of the operation that creates the object. We use object ID to uniquelly identify an object in an Automerge document. The object ID of root is <0, 0>.
Operation Tree
With the growing number of operations in the OpSet, the time consumed for retrieval grows too. Therefore, we divided the OpSet into multiple Operation Tree (OpTree). An OpTree represents the set of operations associated with a specific object, so the number of OpTrees in an OpSet is equivalent to the number of objects in a document.
The reason why we use the term “Tree” is that we use a B-Tree to store it. But conceptually it is a table of operations.
Map
We can begin with a document that includes the Map objects but excludes the List objects.
Basic Idea
Every time we insert a property into a map object, we create an operation like this:
Operation = {
OpId: lamport clock after increment,
ObjId: the objId of the map we're manipulating,
Prop: the property name,
action: "set {someValue}",
}
For example, if we do root.key = A,then we need to insert an operation like this:
{
OpId: <1, 0>
ObjId: <0, 0>
Prop: "key",
action: "set A"
}
When we query a property of a Map object, we simply retrieve the operation manipulating the Map object with highest OpId. That is to say, if we have two operations:
[
{
OpId: <1, 0>
ObjId: <0, 0>
Prop: "key",
action: "set A"
},
{
OpId: <2, 0>
ObjId: <0, 0>
Prop: "key",
action: "set B"
}
]
In this case, root.get("key") will return the operation <2, 0>, and then we can know the value of root.key is B.
OpTree of Map Object
To organize the operations, we use a table, which is OpTree to store the operations associated with a particular object. And the operations in a Map object’s OpTree are sorted by two columns:
- Prop: Operations with the same property are grouped together.
- OpId: If two operations have the same
prop, the operation with the lowerOpIdis placed before the other.
Since an OpTree is sorted by keys, we can use binary search to locate an operation with a particular key, which we will explore in more detail shortly.
Furthermore, there are two additional columns we have not mentioned before: successor and predecessor. In a map object, if operation A is to override another operation B, then we say operation A is a successor of operation B. We can now define an operation as “invisible” if it has a successor.
Example
Let‘s say we have a code snippet in the following:
let mut doc = Automerge::new();
let mut tx = doc.transaction();
tx.put(ROOT, "name", "Alice")?;
tx.put(ROOT, "age", "21")?;
tx.put(ROOT, "age", "23")?;
tx.put(ROOT, "age", "24")?;
tx.put(ROOT, "name", "Bob")?;
tx.commit();
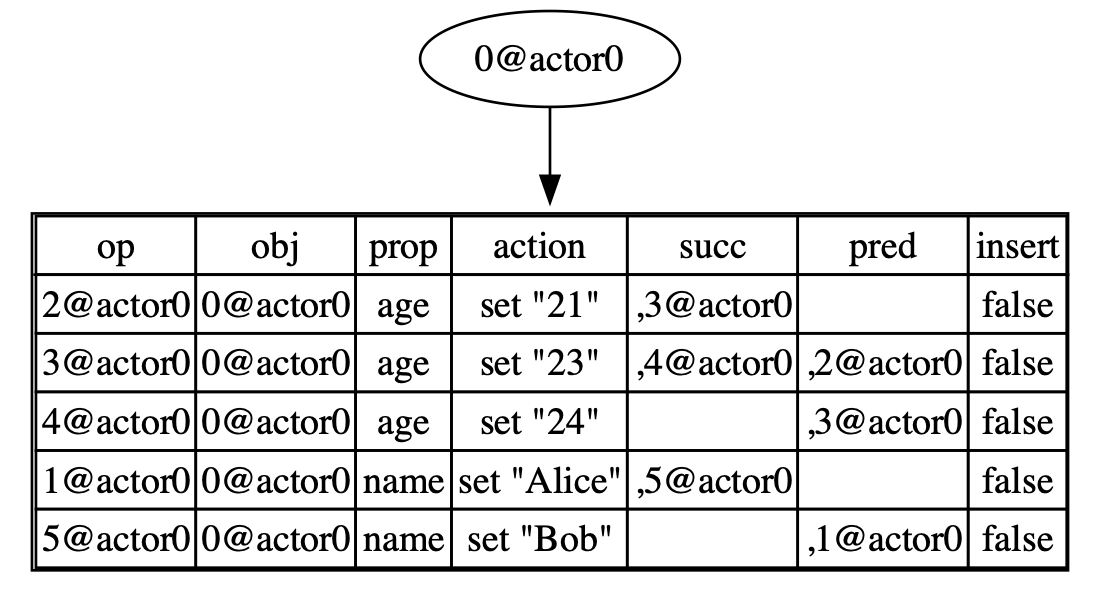
It will result in an OpTree like this:
To query and delete an object in a OpTree, we could use the following code:
let mut tx = doc.transaction();
let name = tx.get(ROOT, "name")?;
tx.delete(ROOT, "age")?;
tx.commit();
Let’s explain how get, put and delete works in pseudocode.
get
def get(table, prop):
operations, _ := search(table, prop);
last := operations[opertaions.len - 1];
return last.action.value;
def search(table, prop):
result := [];
last_index = -1; // "index of the last operation in the result" + 1
start_idx := index of the first row that matches `prop` // binary search
end_idx := index of the last row of the `table`
for i in range(start_idx, end_idx):
if table[i].prop != prop:
return result, i;
if table[i].visible:
result.append(table[i]);
return result, end_idx + 1;
Let’s consider an example of get(root, "name"):
- Initially, we use binary search to locate the starting position of the row where the
propis “name”, which is the row with index 3 in the figure above. Thus:
start_idx = 3;
end_idx = 4;
-
We iterate through
table[3]totable[4]and appendop 5@actor0to theresult. Eventually, thesearchfunction returns([op 5@actor0], 5). -
Finally, in the
getfunction, we return theaction.valueofop 5@actor0, and as a result, we obtain the value ofroot.name, which is “Bob”.
put
def put(table, prop, value):
operations, last_idx := search(table, prop)
pred := []
for operation in operations:
pred.append(operation.op)
local_op := {
op: lamport_clock_inc(),
obj: table.objId,
prop,
action: "set {value}",
pred,
succ: []
}
add_succ(local_op.pred, local_op.op);
insert_op(local_op, last_idx);
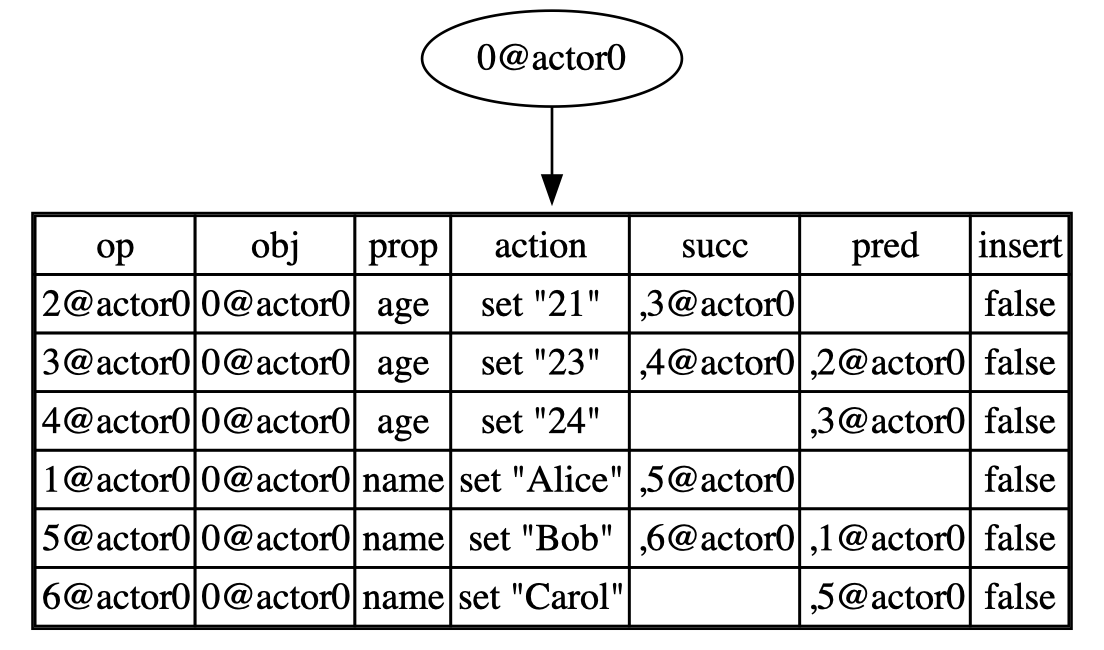
Let’s consider an example of put(root, "name", "Carol"):
- Initially, we use the
searchfunction to search for the predecessor and index, and it returns([op 5@actor0], 5). - Next, a successor is added for
op 5@actor0, which is6@actor0. - Finally,
op 6@actor0is inserted at index 5 of thetable.
delete
def delete(table, prop):
operations, _ := search(table, prop)
pred := []
for operation in operations:
pred.append(operation.op)
new_clock := lamport_clock_inc()
add_succ(pred, new_clock)
Let’s consider an example of delete(root, "age"):
- We use the
searchfunction to find all currently visible operations wherepropisage, and it returns([4@actor0], 3). - We update the successor of
4@actor0to the newly generatedOpId.
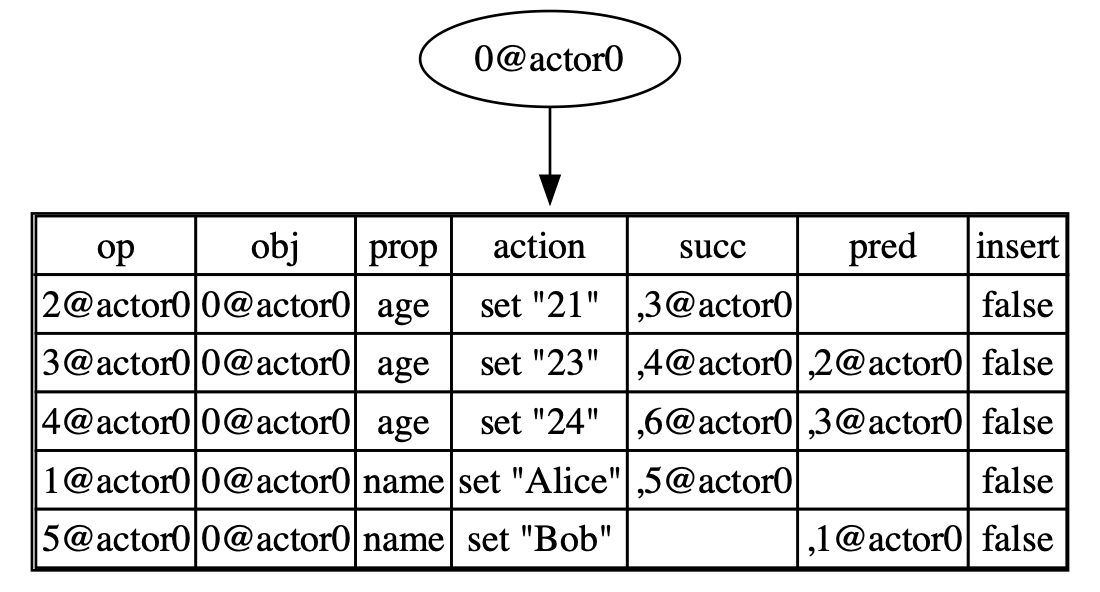
At this point, when we execute get(root, "age"), all operations where prop = age are invisible, so an empty result will be returned, and as a result, age is deleted.
put_object
In order to create a nested map, we also need to support the put_object operation.
def put_object(table, prop, obj_type):
operations, last_idx := search(table, prop)
pred := []
for operation in operations:
pred.append(operation.op)
new_obj_id := lamport_clock_inc();
local_op := {
op: new_obj_id;
obj: table.objId,
prop,
action: "make {obj_type}",
pred,
succ: []
}
add_succ(local_op.pred, local_op.op);
insert_op(local_op, last_idx);
return new_obj_id;
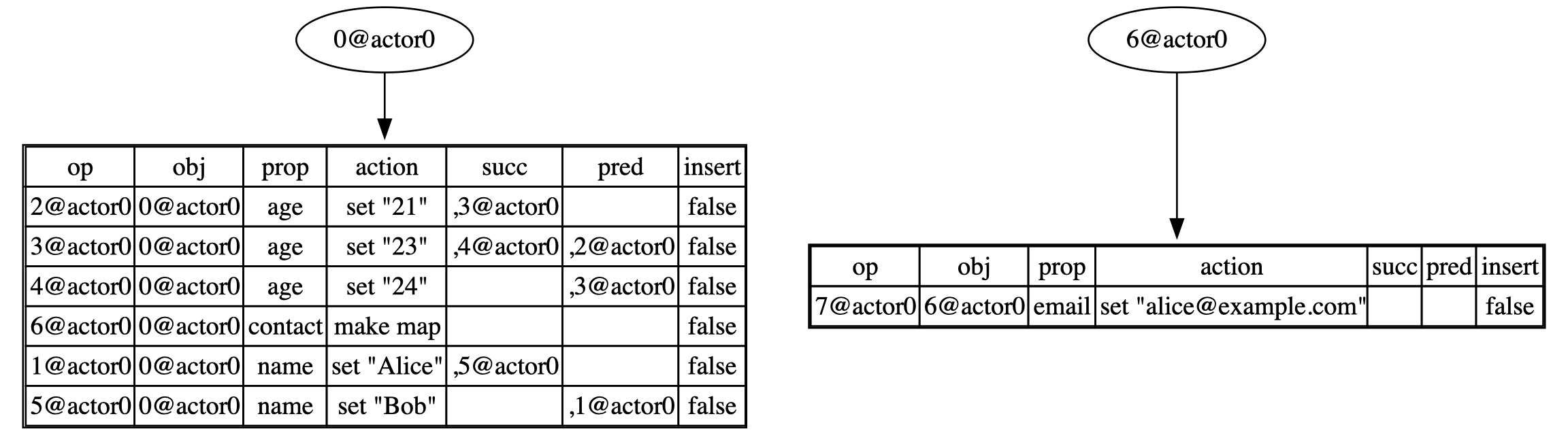
For example, consider the following code snippet:
contact := put_object(root, "contact", Map);
put(contact, "email", "alice@example.com");
- Call the
searchfunction, which returns([], 3)since no contacts exist at the moment. - Generate a
make mapoperation and add it to index 3 of the table. - Function
put_objectreturns the OpId6@actor0, which is the object id of the newly created map. - Using object id
6@actor0, we can access the OpTree ofcontactand insert theput, email, set "alice@example.com"operation into it.
Merge two documents
Merging two documents is equivalent to merging the operations of the two documents and updating the successors if necessary.
Considering the following code:
let mut doc1 = Automerge::new();
let mut tx = doc1.transaction();
tx.put(ROOT, "name", "Alice").unwrap();
tx.put(ROOT, "age", "21").unwrap();
tx.put(ROOT, "age", "22").unwrap();
tx.commit();
let mut doc2 = doc1.fork();
let mut tx = doc1.transaction();
tx.put(ROOT, "age", "100").unwrap();
tx.commit();
let mut tx = doc2.transaction();
tx.put(ROOT, "age", "99").unwrap();
tx.commit();
doc1.merge(&mut doc2)?;
let mut tx = doc1.transaction();
let res = tx.get(ROOT, "age")?;
println!("{:?}", res); // print 99
tx.commit();
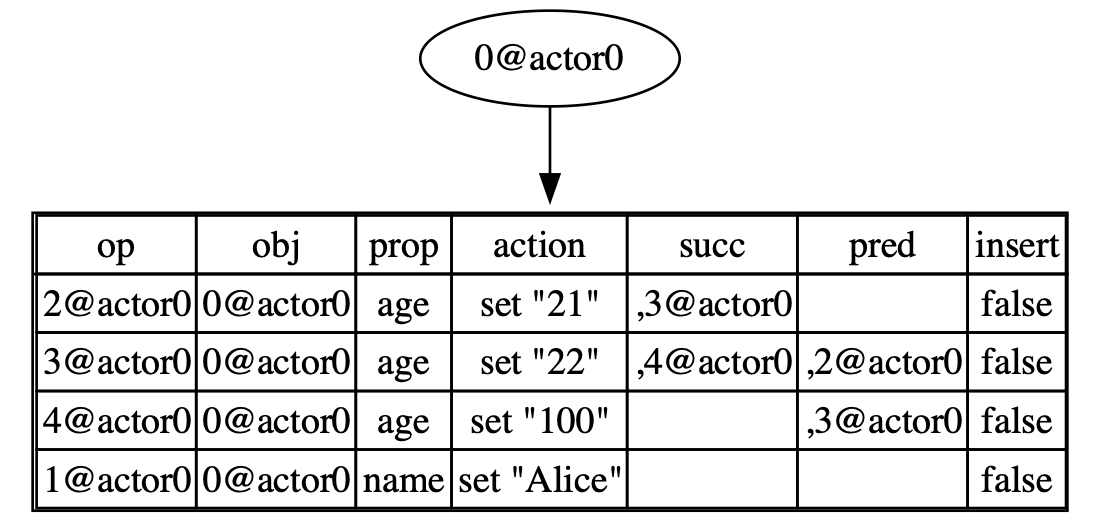
Before merging, doc1 might look like this:
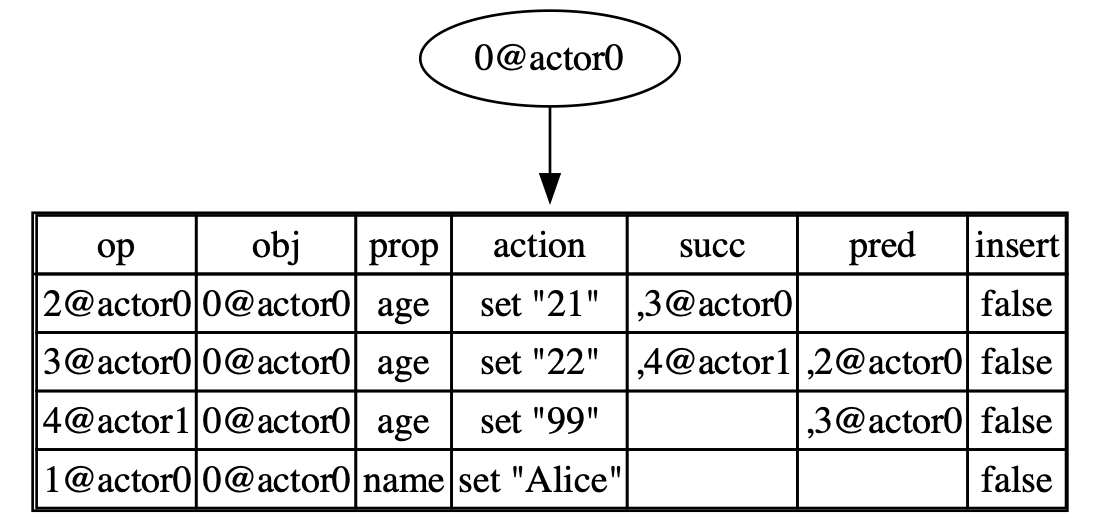
doc2 might look like this:
After merging, the resulting document might look like this:
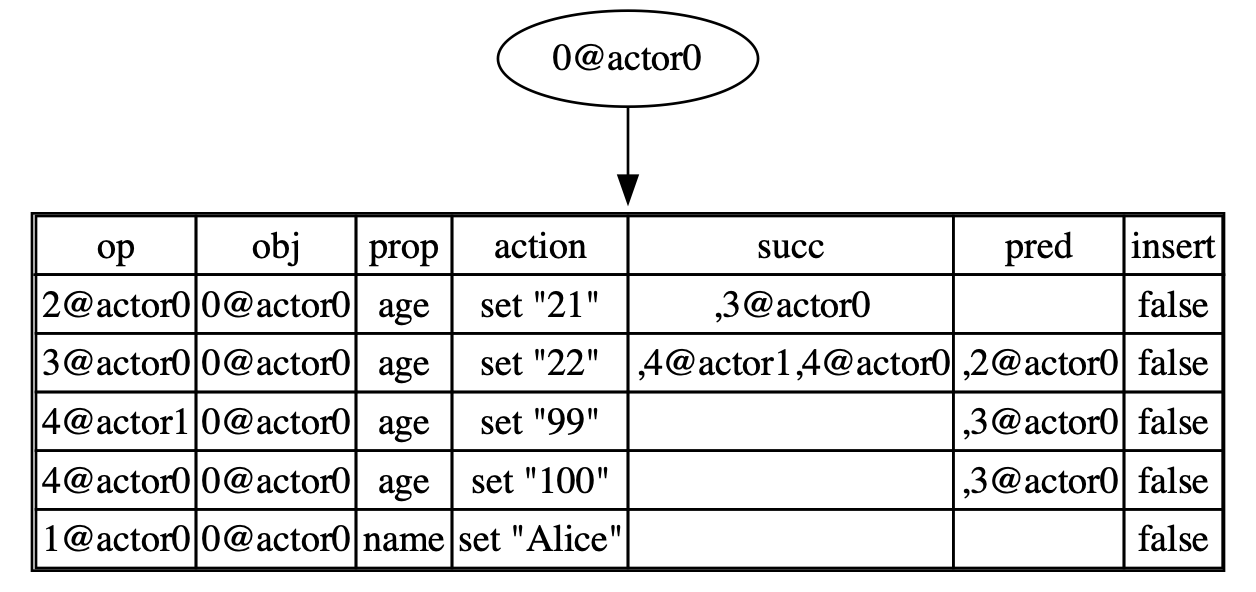
In this case, we merge two documents by adding 4@actor1 from doc2 to doc1, which is missing from doc1. Then, since the predecessor of 4@actor1 is 3@actor0, we need to add 4@actor1 to the successors group of 3@actor0.
At this point, if you call get("age"), the search function will return two operations, 4@actor1 and 4@actor0. Since the get function takes the last operation as the result, it returns 4@actor1, which prints out 99 as the final result.
Furthermore, we have a function called get_all, which we can describe as follows:
def get_all(table, prop):
operations, _ := search(table, prop);
res = [];
for op in operations:
res.append(op.action.value);
return res
In this example, calling get_all(age) will retrieve both 99 and 100. It behaves as a multi-value register.
List
Now we will add the List object to our document. Before we explain how to generate list operations, you need to understand what a Replicated Growable Array is 1.
We need to flatten the RGA tree into a table, just like what we did in Map. This is achieved by performing a Depth First Search (DFS) on the RGA tree. For example, for the following code snippet:
let mut doc1 = Automerge::new();
let mut tx = doc1.transaction();
let list = tx.put_object(ROOT, "list", ObjType::List)?;
tx.insert(&list, 0, "a")?;
tx.insert(&list, 1, "u")?;
tx.insert(&list, 2, "o")?;
tx.insert(&list, 2, "t")?;
tx.put(&list, 0, "A")?;
tx.commit();
We can build the RGA tree like this:
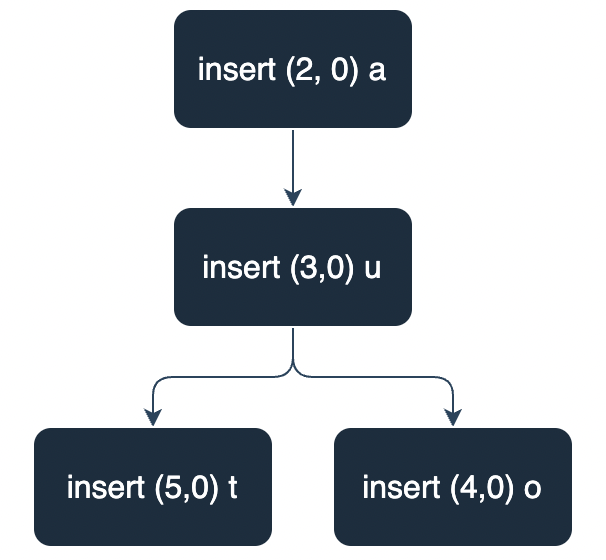
We use DFS to traverse all nodes of the RGA tree and obtain the following table:
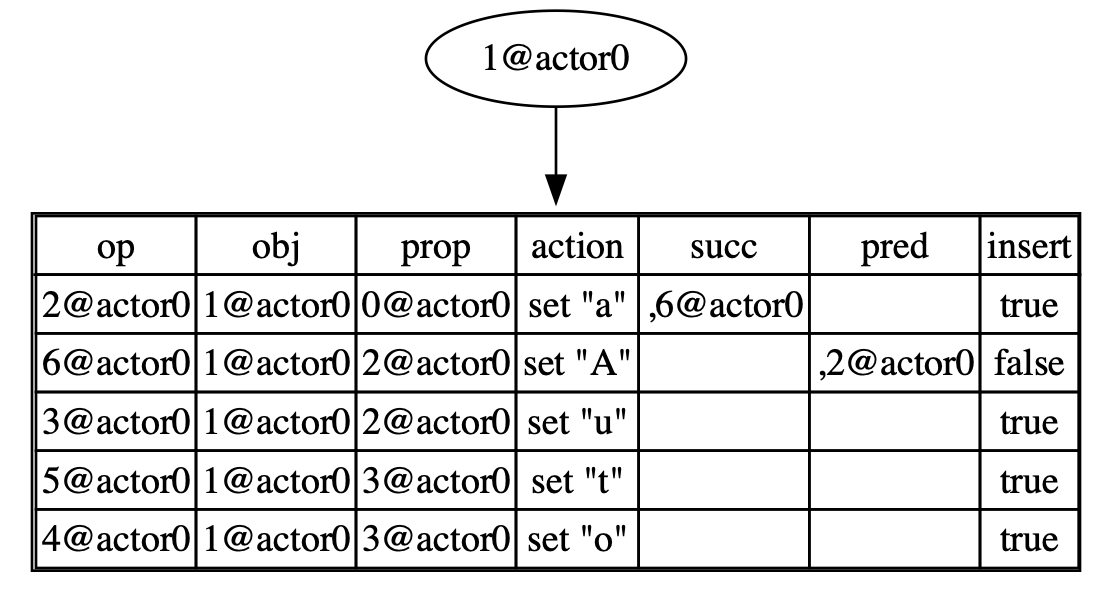
However, the RGA tree is only a conceptual model, and we do not actually maintain a tree in memory. Next, we will describe in pseudocode how to perform get, delete, put, and insert on this table.
Note: the definition of “index” can be confusing when used to refer to both the index of a table and the index of a list interchangeably. To prevent confusion, we will use the term “row number” to indicate the index of a table, while reserving the term “index” specifically for the index of a list.
get
Before diving into the get function, it’s important to note that in the actual implementation of Automerge, tables are implemented using B-trees. This allows for faster query processing. Specifically, we can maintain a variable visible in each node that indicates how many visible elements are in the subtree rooted at that node. If we determine that the element we are looking for is definitely not in the current subtree, we can skip the current subtree entirely.
However, for the sake of simplicity in describing the algorithm, we will assume that no subtrees are skipped. If you are interested in adapating the algorithms to B-Tree, you can delve into the source code for a more detailed understanding.
def get(table, index):
operations, _ := nth(table, index);
last := operations[operations.len - 1];
return last.action.value;
def nth(table, index):
// last element we've ever seen
last_seen = null;
// number of elements in array we've ever seen
seen = 0;
// current position
pos := 0;
// result operations
res = [];
for operation in table:
// If the operation is "insert", we may have a new element traversed (although it's also possible that it's not an element due to a preceding "delete" operation), and in that case, we need to clear the "last_seen" variable.
if operation is insert:
// If we've already seen enough elements, we should return the result
if seen > index:
return res, pos;
last_seen = null;
// it could be a visible insert operation, or a visible put operation
if operation is visible && last_seen is null:
seen += 1;
last_seen = operation;
// if `seen` is greater than `index`, the current operation is what we're searching for
if operation is visible && seen > index:
res.append(operation);
pos++;
return res, pos;
Considering get(list, 2) as an example:
- Start iterating from the beginning and when we reach index 4,
seenis equal to 3. So we addoperation 5@actor0to thereslist. - Return the result, which is
([5@actor0], 4). - By reading the value of
operation 5@actor0, we get the final resultt.
delete
def delete(table, index):
operations, _ := nth(table, index);
pred := []
for operation in operations:
pred.append(operation.op)
add_succ(pred, lamport_clock_inc());
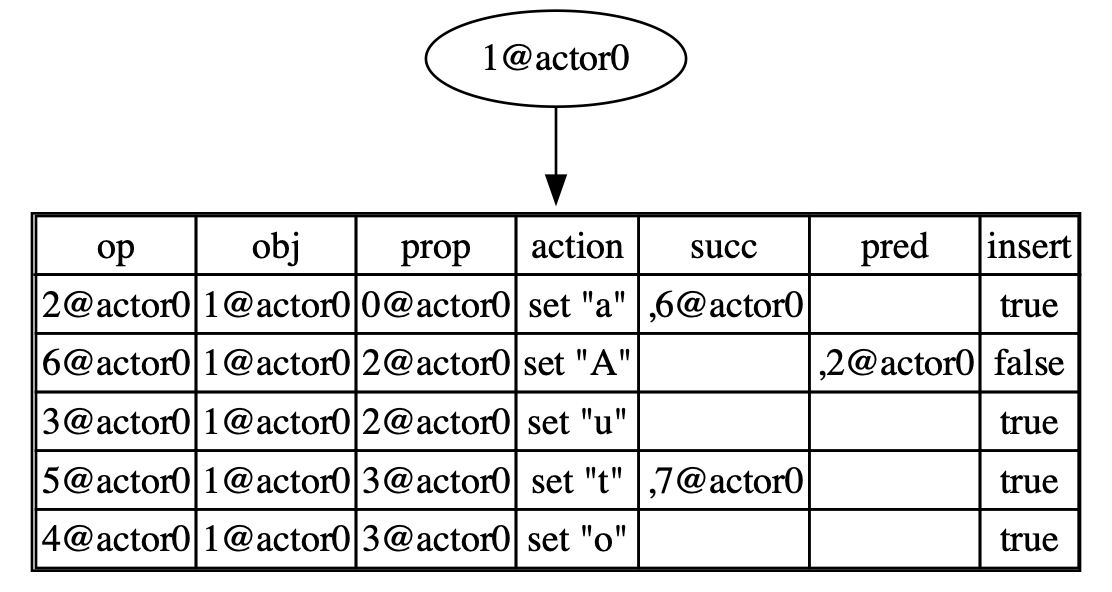
Considering delete(list, 3) as an example:
- By calling the
nthfunction, we obtain([5@actor0], 4). - We updated the successor of
5@actor0to the newly generated OpId7@actor0.
put
def put(table, index, value):
operations, pos := nth(table, index);
first := operations[0];
if first is insert:
prop := first.op;
else:
prop := first.prop;
pred := []
for operation in operations:
pred.append(operation.op)
local_op := {
op: lamport_clock_inc(),
obj: table.objId,
prop,
action: "set {value}",
succ: null,
pred,
insert: false,
}
add_succ(pred, local_op.op);
insert_op(local_op, pos);
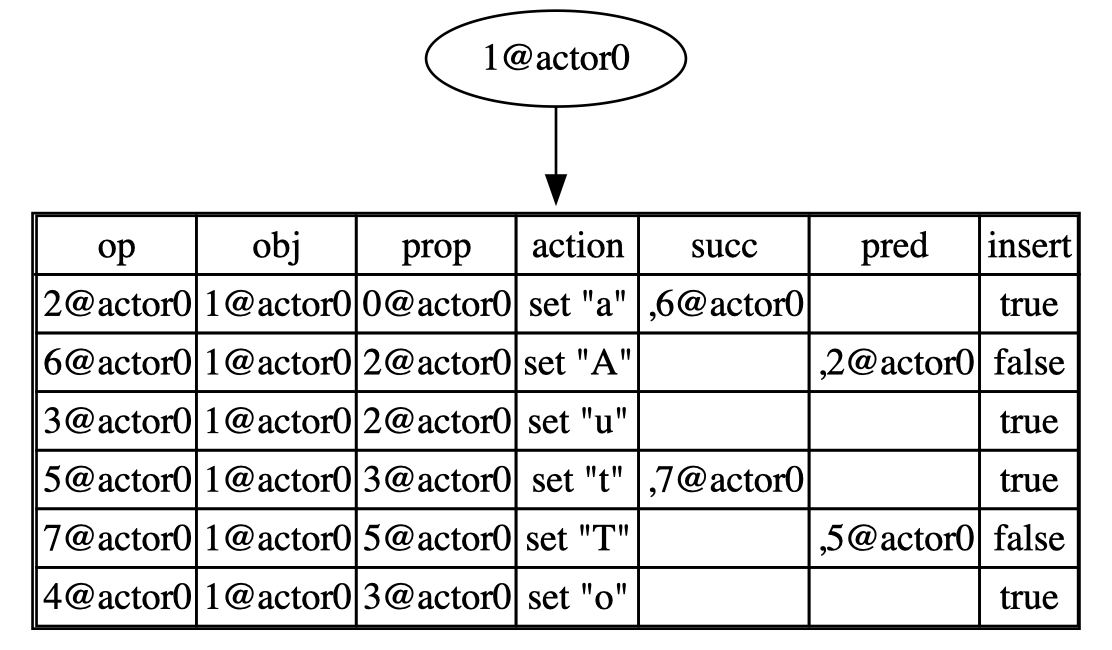
Considering put(2, "T") as an example:
- By calling the
nthfunction, we obtain([5@actor0], 4). - Add successor for
op 5@actor0, which is7@actor0. - Finally,
op 7@actor0is inserted at row number 4 of the table.
insert
def insert(table, index, value):
insert_row_number, insert_prop := insert_nth(table, index);
local_op := {
op: lamport_clock_inc(),
obj: table.objId,
prop: insert_prop,
action: "set {value}",
succ: null,
pred: null,
};
insert_op(local_op, insert_row_number);
def insert_nth(table, index):
// row number to be inserted at
insert_row_number := -1;
// prop of the operation to be inserted
insert_prop := null;
// last element we've ever seen
last_seen := null
// number of elements we've ever seen
seen := 0
// current position
pos := 0
for operation in table:
// If the operation is "insert", we may have a new element traversed (although it's also possible that it's not an element due to a preceding "delete" operation), and in that case, we need to clear the "last_seen" variable.
if operation is insert:
// If we've already seen enough elements, the current position is the position to be inserted at
if insert_row_number == -1 && seen >= index: // greater than or equal
insert_row_number = pos;
last_seen = null;
// it could be a visible insert operation, or a visible put operation
// update seen, last_seen and insert_prop
if operation is visible && last_seen is null:
// if we've already seen enough elements, return the insert index and prop
if seen > index:
return insert_row_number, insert_prop
seen += 1;
last_seen = operation;
if operation is insert:
insert_prop := operation.op;
else:
insert_prop := operation.prop;
pos++;
// if index exceeds the table
insert_row_number = last row number of the table plus 1
insert_prop = last insert operation of the table
return insert_row_number, insert_prop
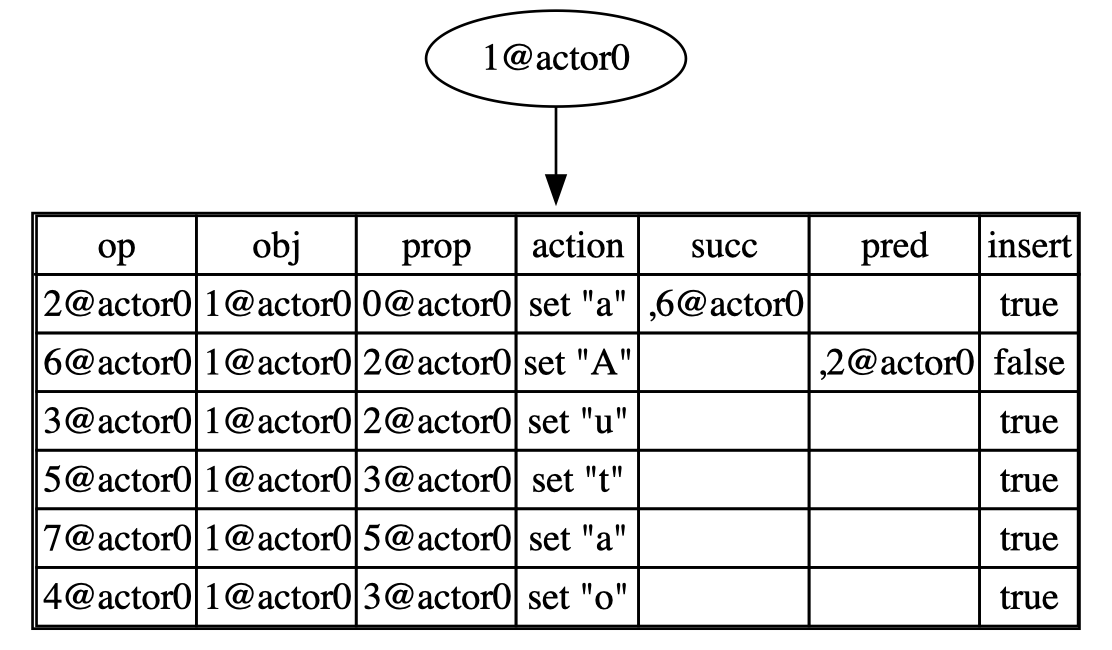
Considering insert(3, "a") as an example:
- When iterating to index 3, update the
insert_propas5@actor0. - When iterating to index 4, update the
insert_row_numberas 4. - Construct an insert operation and insert it at row number 4.
Merge two documents
Like in maps, merging two documents is conceptually taking the union of two OpSets. Let’s consider the following code snippet:
let mut doc1 = Automerge::new();
let mut tx = doc1.transaction();
// auto
let list = tx.put_object(ROOT, "list", ObjType::List)?;
tx.insert(&list, 0, "a")?;
tx.insert(&list, 1, "u")?;
tx.insert(&list, 2, "o")?;
tx.insert(&list, 2, "t")?;
tx.put(&list, 0, "A")?;
tx.commit();
// matic
let mut doc2 = doc1.fork();
let mut tx = doc2.transaction();
tx.insert(&list, 4, "m")?;
tx.insert(&list, 5, "a")?;
tx.insert(&list, 6, "t")?;
tx.insert(&list, 7, "i")?;
tx.insert(&list, 8, "c")?;
tx.commit();
// merge
let mut tx = doc1.transaction();
tx.insert(&list, 4, "m")?;
tx.insert(&list, 5, "e")?;
tx.insert(&list, 6, "r")?;
tx.insert(&list, 7, "g")?;
tx.insert(&list, 8, "e")?;
tx.commit();
// automaticmerge
doc1.merge(&mut doc2)?;
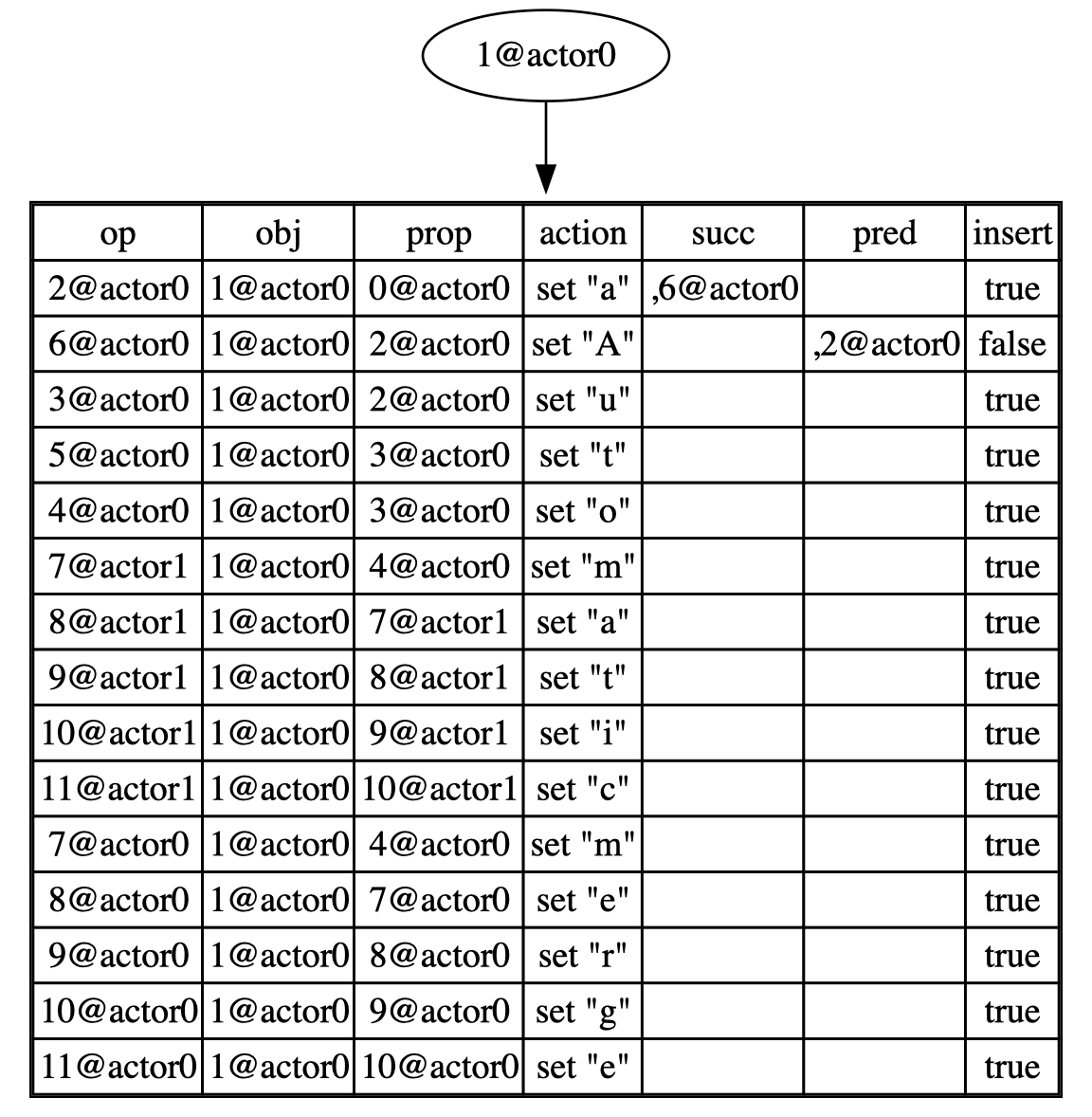
for (i, val1, id) in doc1.list_range(&list, ..) {
let val2 = doc1.get(&list, i)?;
println!("{:?}", val2);
}
doc1 before merging:
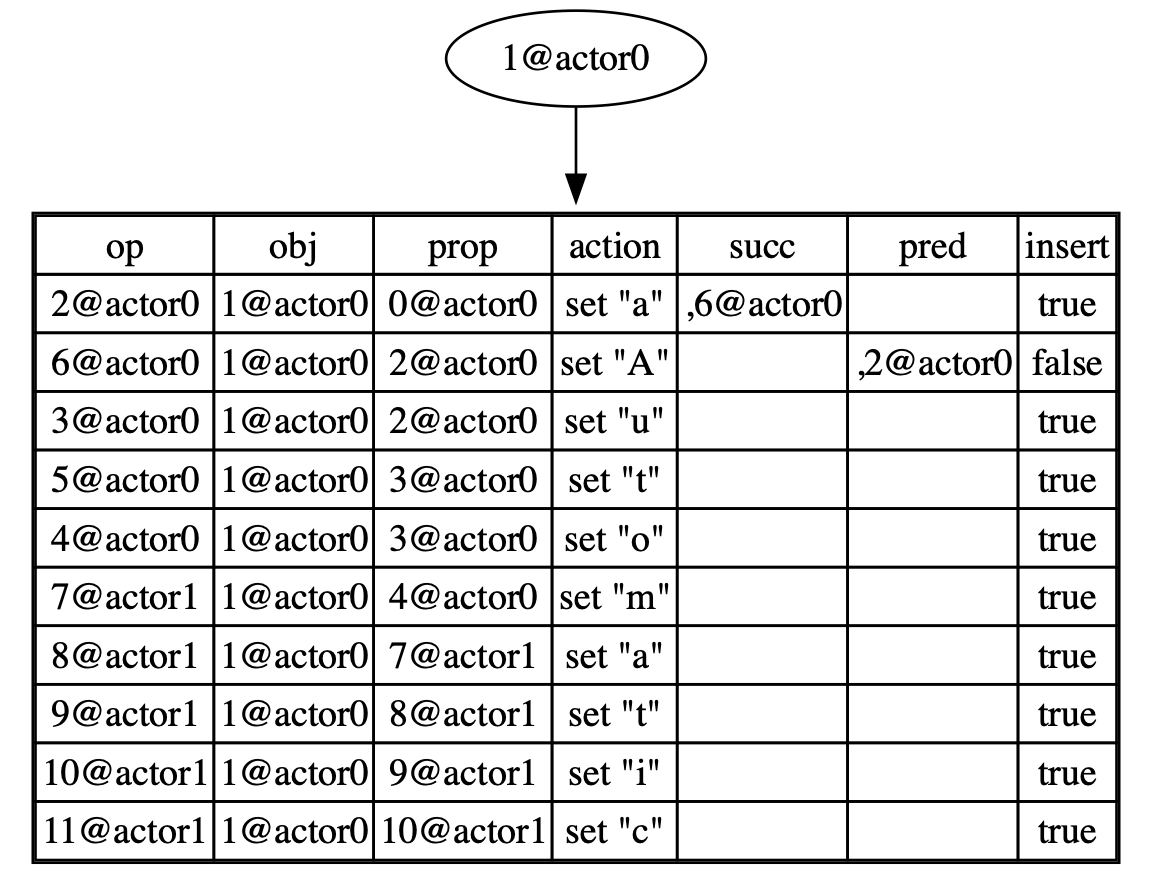
doc2 before merging:
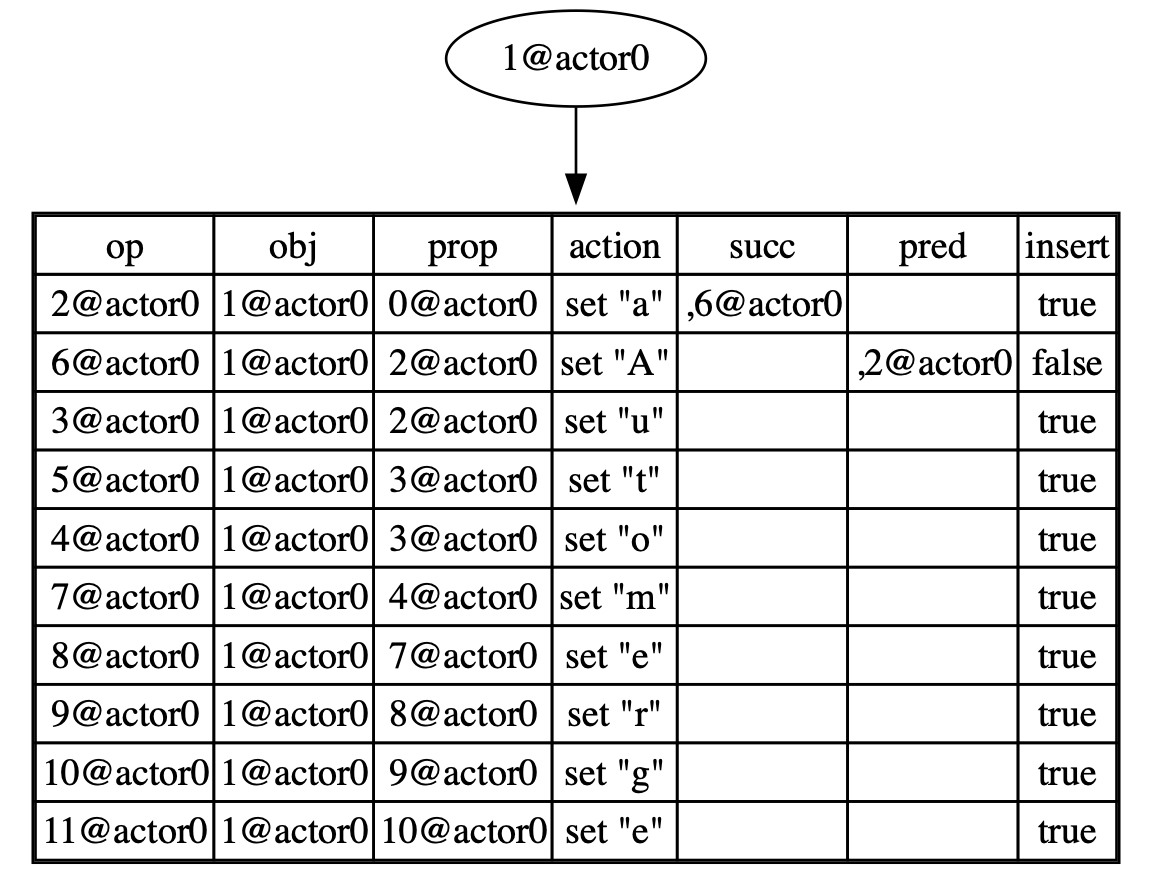
After merging:
Reference
[1] H.-G. Roh, M. Jeon, J.-S. Kim, and J. Lee, “Replicated abstract data types: Building Blocks for Collaborative Applications,” Journal of Parallel and Distributed Computing, vol. 71, no. 3, pp. 354–368, 2011. doi:10.1016/j.jpdc.2010.12.006